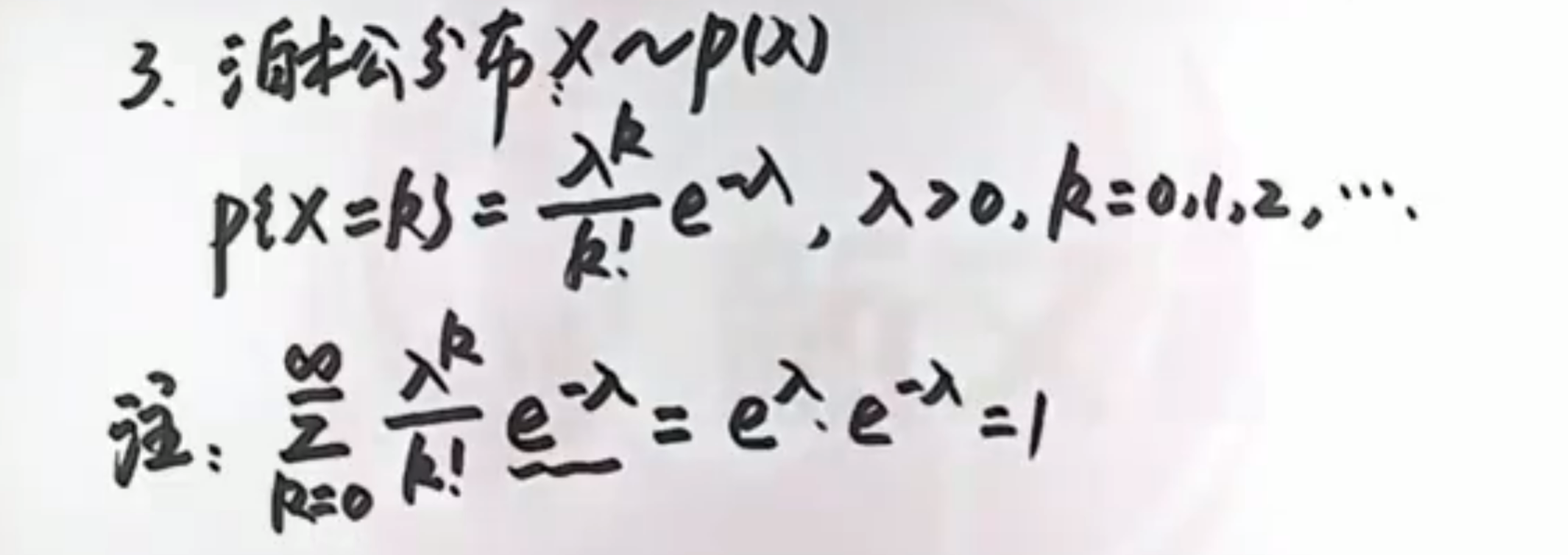概率论

离散型随机变量

This place only note practical for me,文章中的图片可能访问速度比较慢，可以刷新重新加载

  1. 需要注意离散型随机变量点概率不同，范围概率是后附带前
  2. 常见离散型
    1. 0-1分布
    2. 二项分布
    3. 泊松分布（出现条件使某二者概率相等即可求出未知λ）
    4. 几何分布
    5. 超几何分布
  3. 泊松定理（使用点在于样本量远大于概率，此时再使用二项分布就很难计算，这时可以转换成泊松分布便于计算）

    连续型随机变量


    作为f(x)成为密度需要满足的条件有两个，这一般也是题目求未知量的求解条件

对于密度，几乎处不相等，但是这是不做区分的，就是闭区间和开区间视为相同

出现F(x)如何求f(x)?

求概率密度的方式：

浅来一个小栗子：

几何方式：


对于这类题型，思路是一致的，首先是运用定义求解未知数，然后通过变现积分的方式求解分布函数，建议使用几何法，将图做出，对x进行区间讨论更为直观

常见连续型

  1. 均匀分布

    一个常见的坑

    注： 概率是永远无法推出事件的关系的

  2. 指数分布

    背景：

  3. 正态分布
    正态分布的标准化

一般出现P(X>a)对其转化为1-P(X<=a)的形式，这样是分布函数方便进行计算
小栗子：
标准做法：

求函数的分布

【思考】什么是分布？
就是在平面几何上面积的分布情况，此时会出现各种条件，这些条件就是为了区分出不同的条件，不同的面积区间，去分析

离散型

连续型

此时有三种情况

下面两种关键点在于如何求解分布律

连续型栗子：

做这种题的思路：
首先分析边界值，求出二者的分布律，之后去进行判断空集和1，第二步开始求最关键的分布律，此时同样是根据图形进行观察而非单纯求解不等式，观察Y处于下方的位置求解出x的范围，求解出分布律，求出之后不用先积分在进行求导，这是一个互逆的过程，所以可以选择直接使用变限积分的方式

混合型：


虽然是混合型，但是流程也是一样的，思路不变

第三章 二维随机变量及其分布

正式学习前先考虑几个问题：
什么是多维r.v.

联合分布函数是什么？

多维r.v.性质：


二维离散型随机变量

接下来进入正式学习：

对于这类形式又是如何求对应概率的呢？
直接上个小栗子：

知道单个随机变量的分布率相当于知道了边缘分布，此时需要进行下一步对条件进行分析，只存在一个条件，我们必须对其进行转化，那么该如何转化，这里是非，很容易想到对立事件

p.s.

条件分布律

对于单行单列也同样满足规范性和非负性，也为条件分布律

二维连续型随机变量（使用二重积分）

求解分布密度函数（f(x,y)的求解）

充要条件:

如何求概率？

小栗子：

求解：

可能出现的误区：二重积分的几何意义是体积而不是面积


做完可以发现，这几问给的条件不同，但是解题时都是进行二重积分的运算，不同的条件导致的只是x,y的取值范围发生变化
类似第三问可以推出一个公式P(Z) Z=F(x,y)，但是都是同样的思路解题

边缘密度


补栗子：

小插曲

对于x区间已知或者y区间已知去判断其它区间，比如x已知固定范围，那么此时做一条垂直x的线，从小往大积分，区分区间即可

条件密度



而x本身不是均匀分布

但此时y不是均匀分布

随机变量的独立性问题

什么是独立？

那么如何判定？

  1. 离散型
  2. 连续型

简单的小tips：快速判断是否独立
条件1：正矩形 （边平行坐标轴的矩形）
条件2：f(x,y)可分离变量，即可以将x，y单独拆离出来成为和另外一个数相乘的形式

补充小知识点：
U(),E() 中的参数分别代表，均匀分布的参数范围和λ的值
N（）中的参数含义：括号内（A，B），A代表题目中trial的平均值，B代表方差。在一个随机的正态分布转换为标准正态分布的时候，注意我们要考虑的是标准差，而非方差

小栗子：

条件独立性实际上就是告诉联合密度的值，知道这个之后如果需要求什么值就可以结合之前学过方式使用二重积分求解

两个重要结论：

p.s. p42

二维均匀分布

what?how?

栗子：

二维正态分布

了解参数含义：

相关系数条件

由(X,Y)的分布，求Z=g(X,Y)的分布

  1. 二维离散型
    小栗子：
  2. 二维连续型
    Z是一维随机变量，可能性有三种

对于连续型这里提出几个思路方法：

  • 分布函数法

    可以使用暴力求导的方式
    注意这里的g(z,x)的求导是对z求偏导，后续的g(z,（x）)就是将x给替换成这个函数式
    栗子：

    解答：



    括号2：
    分析过程

    剩下计算部分为暴力求解法

    仅做记录
    出现一个结论：

  • max{X,Y},min{X,Y}的分布
    背景


    关于min{}的推导，使用到概率公式

    关于min，max(X,Y)的结论

第四章 数字特征

  1. 数学期望 又称为均值
    什么是期望？
    定义：

期望又分为离散型：

来颗小栗子：

栗二是泊松分布

几何分布

以及连续型：

  1. 均匀分布

  2. 指数分布

    小坑，区分清楚题给条件参数还是均值

  3. 正态分布
    具有对称性的函数可以运用奇偶性，但前提是该积分收敛

如何去求函数的期望？
这里同样是分为离散型和连续型
对于离散型这两种方式都可以

但是对于连续型尽量是使用X的分布去求解

方差的计算：
几何分布

正态分布：

整体记忆：

对二维随机变量：
离散型的求解方式

连续型的小栗子：


这里是借助了奇偶性
再来颗栗子：

如果出现一个直接带即可，如果出现的是f(x,y)那么需要两个范围都出现

注意： （关于独立和期望的关系）

期望的性质

线性关系：无法相互推出

方差 （反映X对EX的偏离的大小）

表达式：

注意：平方的期望>=期望的平方

变形使用：

性质：

对于二项分布的方差证明：（运用到了分解的思想）

协方差

定义以及计算方式

性质：

关于性质1的坑

可以分配

来颗小栗子：

解法：


这里复习了离散型的期望求法

相关系数

定义：
反映出了XY的线性关系的紧密程度

相关系数为0时，不一定独立

性质：

  1. 必然小于1

来颗栗子：

在计算时将题给条件的表转化为这种表的形式方便计算
从这题可以看出判断是否相关以及判断独立完全是两个不同的证明方式

栗2：

栗3：

栗4：

矩

第五章 大数定律和中心极数定理

  1. 切比雪夫不等式
    直接上例题

    解：
  2. 依概率收敛
    存在的考向：
  3. 大数定律（无需严格证明）


小栗子：

  1. 中心极限定理

第六章 数理统计


关于出现一句话，相当于给出两个条件这件事

小栗子（关于同分布独立性的应用）：

统计量

样本均值，样本方差

样本k阶原点矩

样本中心矩

顺序统计量

各种分布

小栗子：



栗子：（解决卡方分布如何构造的问题）

思路：首先是由其中的方差进行运算，将两个参数的方差分别求出，写出卡方形式，之后构造出卡方即可求出对应未知数

t分布

小栗子:

F分布

性质：

综合小栗子：（判断分布）

对于样本的方差值是可以相加的，相加之后本身除以自身的标准差，结果就是标准正态分布
分母带上根号一般就是t分布

抽样分布（正态分布下）


小栗子：

解：

选项d是因为并不独立x2和x2

第七章

矩估计的方式：

最大似然估计
似然函数：样本取到观测值的概率
思想：概率越大，出现的频率越高
栗子：

这里是第一步，写出似然函数

关于似然估计的求解步骤

下面做举栗（还是上面那题，外加一个求解似然估计值）:


栗子2：

举个离散型：

关于离散型x平均值是可以求出的，让其和概率相等即可

无偏估计


就是一个概念，见下题，就是一个期望的变化

做题记录：


  1. 从选项反向分析，看到条件概率先写出对应方程式，将题目所给条件转化即可迎刃而解，这里对我的提醒就是条件概率不熟悉
    A属于B，B非空，则AB交集为A
    且记住概率的值永远小于1
    故选B

P (AB)表示A和B同时发生的概率,如果A,B相互独立,则P (AB)=P (A)P (B); 如果A,B不是相互独立,则P (AB)=P (B|A)P (A)。

全概率公式和贝叶斯公式使用的条件分别是前者是一个结果由不同条件导出，而后者是从结果反推是那种情况
贝叶斯说白了就是这种条件占总体的多少


  1. 关于这题：积累的就是给出偶函数给出的是对称条件，结果就是概率为1/2，区间分别为（0，+无穷）（-无穷，0）
    这里是计算（-无穷，-a）区间的密度，那么需要对其进行转化，进行一步换元，这里又使用了一个性质，区间可以被拆分相加，这是一个连续的过程

记住一个小结论：


  1. 对于这题需要注意一个点就是x，y的取值范围，不能直接想当然的认为都是（0，1）之间


  2. 由联合概率密度求联合分布函数，重点有二：讨论自变量的取值&确定有效的积分范围
    还有注意这个公式，是需要分段的


  3. 几何概型经典（约会问题）
    考察线性规划